
拓?fù)湮锵嗟闹饕卣鳛槟芟堕g存在受體拓?fù)浔Wo(hù)的邊界態(tài),這類物態(tài)通常由定義在整個(gè)布里淵區(qū)內(nèi)的拓?fù)洳蛔兞靠坍?huà)。近年來(lái),一類新型的高階拓?fù)湎嗍艿綇V泛關(guān)注,其中,具有n階拓?fù)湫再|(zhì)的d維系統(tǒng),其拓?fù)溥吔鐟B(tài)局域在系統(tǒng)的(d-n)維邊界上。與傳統(tǒng)拓?fù)湎嘞啾龋斑吔绲倪吔纭蓖負(fù)鋺B(tài)可能同時(shí)涉及到系統(tǒng)體態(tài)及低維邊界態(tài)的拓?fù)湫再|(zhì),具有更豐富的體邊對(duì)應(yīng)關(guān)系及拓?fù)浞诸悺5壳埃瑢?duì)高階拓?fù)湎嗟耐負(fù)淇坍?huà)大都依賴于具體模型的空間對(duì)稱性,仍缺乏一個(gè)可直接通過(guò)實(shí)驗(yàn)探測(cè)的普適性拓?fù)淇坍?huà)理論。
近日,我校物理與天文學(xué)院量子工程與精密測(cè)量團(tuán)隊(duì)李林虎副教授與新加坡國(guó)立大學(xué)的龔江濱教授及朱偉偉博士合作,針對(duì)復(fù)對(duì)稱類高階拓?fù)湎啵岢隽艘惶谆趧?dòng)力學(xué)的嵌套拓?fù)淇坍?huà)理論。該理論基于系統(tǒng)動(dòng)量空間哈密頓量定義了一系列互相嵌套的“能帶反轉(zhuǎn)面”(band inversion surfaces),系統(tǒng)整體的高階拓?fù)湫再|(zhì)由這些能帶反轉(zhuǎn)面分別對(duì)應(yīng)的拓?fù)洳蛔兞考跋嗷デ短钻P(guān)系決定(見(jiàn)圖1)。特別的,通過(guò)這種方式定義的拓?fù)洳蛔兞浚芍苯佑上到y(tǒng)贗自旋紋理的卷繞性質(zhì)給出,并可通過(guò)量子淬火動(dòng)力學(xué)中系統(tǒng)的長(zhǎng)時(shí)間演化進(jìn)行測(cè)量。同時(shí),這套高階拓?fù)淇坍?huà)方案不依賴于系統(tǒng)的空間對(duì)稱性,適用于滿足克利福德代數(shù)(Clifford algebra)的任意高階拓?fù)湎唷_@項(xiàng)工作將不受空間對(duì)稱性保護(hù)的高階拓?fù)湎噙@一概念,拓展到了任意維度任意拓?fù)潆A數(shù)的一整類高階拓?fù)湎啵⑻岢隽艘惶灼者m的拓?fù)淇坍?huà)理論,極大地加深了對(duì)高階拓?fù)湎嗟恼J(rèn)識(shí)。此外,該工作所提出的拓?fù)淇坍?huà)方案亦可以在超冷原子及固態(tài)量子比特等多種量子模擬平臺(tái)中通過(guò)動(dòng)力學(xué)性質(zhì)來(lái)測(cè)量,為實(shí)驗(yàn)上研究高階拓?fù)湎嗵峁┝吮憷?/p>
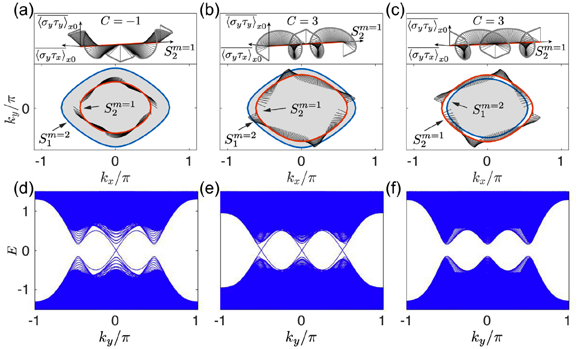
圖1:當(dāng)系統(tǒng)的能帶反轉(zhuǎn)面按順序嵌套時(shí)(a,b),系統(tǒng)中存在類手征高階拓?fù)溥吔鐟B(tài)(d,e),其數(shù)量由不同能帶反轉(zhuǎn)面上贗自旋卷繞數(shù)確定。當(dāng)能帶反轉(zhuǎn)面不按順序嵌套時(shí)(c),系統(tǒng)不存在高階拓?fù)溥吔鐟B(tài)(f)。
該成果以“Direct dynamical characterization of higher-order topological phases with nested band inversion surfaces”為題在線發(fā)表在中科院一區(qū)期刊Science Bulletin上,李林虎副教授為第一作者,新加坡國(guó)立大學(xué)龔江濱教授為通訊作者。該研究得到了廣東省量子精密測(cè)量與傳感重點(diǎn)實(shí)驗(yàn)室的大力支持。